Our Products

This Problem Soltion  

Introduction:

In this assignment, you will determine all possible flight plans for a person wishing to travel between two different cities serviced by an airline (assuming a path exists). You will also calculate the total cost incurred for all parts of the trip. For this assignment, you will use information from two different input files in order to calculate the trip plan and total cost.

1.      Origination and Destination Data – This file will contain a sequence of city pairs representing different legs of flights that can be considered in preparing a flight plan. For each leg, the file will also contain a dollar cost for that leg and a time to travel[1]. For each pair in the file, you can assume that it is possible to fly both directions.

2.      Requested Flights – This file will contain a sequence of origin/destination city pairs. For each pair, your program will determine if the flight is or is not possible. If it is possible, it will output to a file the flight plan with the total cost for the flight. If it is not possible, then a suitable message will be written to the output file.

The names of the two input files as well as the output file will be provided via command line arguments.

Flight Data:

Consider a flight from Dallas to Paris. It’s possible that there is a direct flight, or it may be the case that a stop must be made in Chicago. One stop in Chicago would mean the flight would have two legs. We can think of the complete set of flights between different cities serviced by our airline as a directed graph. An example of a directed graph is given in Figure 1.

In this example, an arrow from one city to another indicates the direction of travel. The opposite direction is not possible unless a similar arrow is present in the graph. For this programming challenge, each arrow or flight path would also have a cost associated with it. If we wanted to travel from El Paso to city Chicago, we would have to pass through Detroit. This would be a trip with two legs. It is possible that there might not be a path from one city to another city.  In this case, you’d print an error message indicating such.

In forming a flight plan from a set of flight legs, one must consider the possibility of cycles. In Figure 1, notice there is a cycle involving Chicago, Fresno, and Greensboro. In a flight plan from city X to city Y, a particular city should appear no more than one time.

The input file for flight data will represent a sequence of origin/destination city pairs with a cost of that flight. The first line of the input file will contain an integer which indicates the total number of origin/destination pairs contained in the file.

Figure 1 - Sample Directed Graph

Sample Data

Flight Data:

Here is an example of a flight data input file (it is not one that goes with Figure 1):

4

Dallas|Austin|98|47

Austin|Houston|95|39

Dallas|Houston|101|51

Austin|Chicago|144|192

The first line of the file will contain an integer indicating how many rows of data will be in the file.  Each subsequent row will contain two city names, the cost of the flight, and the number of minutes of the flight.  Each field will be separated with a pipe (shift-\ on most keyboards).

Requested Flight Plans:

A sample input file for requested flight plans is shown below.  The first line will contain an integer indicating the number of flight plans requested.  The subsequent lines will contain a pipe-delimited list of city pairs with a trailing character to indicate sorting the output of flights by time (T) or cost (C).  Your solution will find all flight paths between these two cities (if any exists) and calculate the total cost of the flights and the total time in the air.

2

Dallas|Houston|T

Chicago|Dallas|C

Output File:

For each flight in the Requested Flight Plans file, your program will print the three most efficient flight plans available based on whether the request was to order by time or cost.  If there are fewer than three possible plans, output all of the possible plans.  If no flight plan can be created, then an error message should be output. Here is an example:

Flight 1: Dallas, Houston (Time)

Path 1: Dallas - Houston. Time: 51 Cost: 101.00

Path 2: Dallas - Austin - Houston. Time: 86 Cost: 193.00

Flight 2: Chicago, Dallas (Cost)

Path 1: Chicago - Austin - Dallas. Time: 237 Cost: 242.00

Path 2: Chicago - Austin - Houston - Dallas. Time: 282 Cost: 340.00

Implementation Details and Requirements:

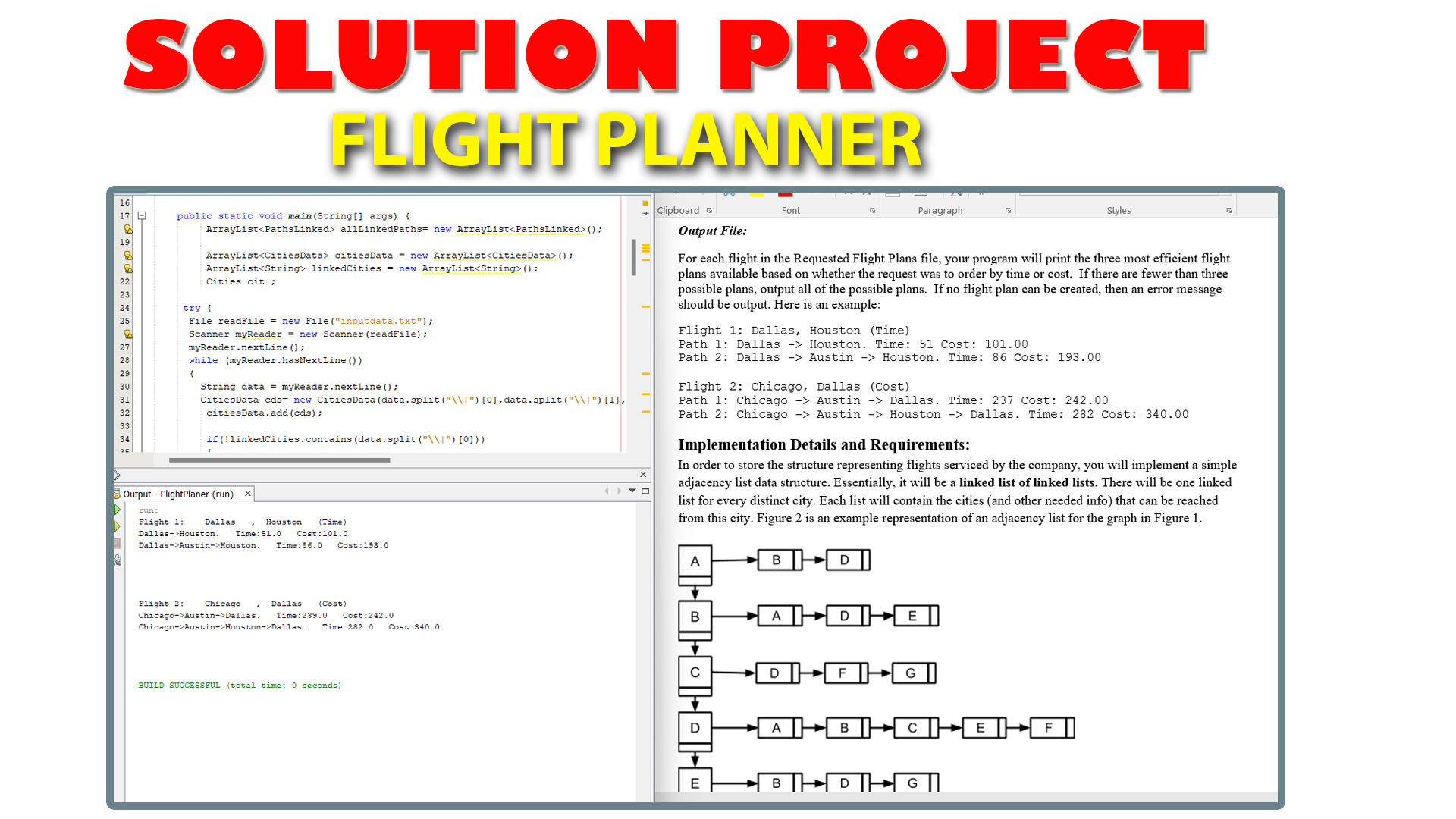
In order to store the structure representing flights serviced by the company, you will implement a simple adjacency list data structure. Essentially, it will be a linked list of linked lists. There will be one linked list for every distinct city. Each list will contain the cities (and other needed info) that can be reached from this city. Figure 2 is an example representation of an adjacency list for the graph in Figure 1